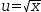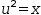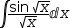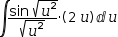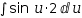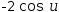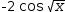4.4.2 U-Substitution
U-substitution
is used for integrands in which one product term is the derivative of
the other product term. That is, the integral has the form
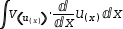 ∫v(u(x))⋅ⅆu(x)ⅆx ⅆx. When U-Substitution (see §3.4.1) is applied to a subexpression of the integrand, the integrand is
transformed by replacing the subexpression with a placeholder
variable, often u, and dividing the integrand by the derivative of the
subexpression with respect to the original integrator. For an
expression like
∫v(u(x))⋅ⅆu(x)ⅆx ⅆx. When U-Substitution (see §3.4.1) is applied to a subexpression of the integrand, the integrand is
transformed by replacing the subexpression with a placeholder
variable, often u, and dividing the integrand by the derivative of the
subexpression with respect to the original integrator. For an
expression like
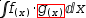 ∫f(x)⋅.{g(x)} ⅆx, u-substitution produces
∫f(x)⋅.{g(x)} ⅆx, u-substitution produces
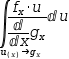 ∫f_x⋅u÷ⅆg_xⅆx ⅆ(u(x)→g_x).
∫f_x⋅u÷ⅆg_xⅆx ⅆ(u(x)→g_x).
If u has been chosen appropriately,
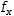 f_x
f_x
and
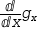 ⅆg_xⅆx
ⅆg_xⅆx
will cancel, resulting in a simpler integral in terms of u. Moreover,
the correspondence between the original subexpression and u is
perpetuated in a decoration of the form
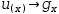 u(x)→g_x
u(x)→g_x.
Try this for
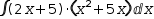 ∫(2⋅x+5)⋅(x^2+5⋅x) ⅆx. Here,
∫(2⋅x+5)⋅(x^2+5⋅x) ⅆx. Here,
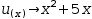 u(x)→x^2+5⋅x
and
u(x)→x^2+5⋅x
and
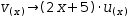 v(x)→(2⋅x+5)⋅u(x). The derivative of the second product term in the integrand matches the first product
term.
v(x)→(2⋅x+5)⋅u(x). The derivative of the second product term in the integrand matches the first product
term.
Select the second product term  ∫(2⋅x+5)⋅(.{x^2+5⋅x.}) ⅆx and apply U-Substitution to produce
∫(2⋅x+5)⋅(.{x^2+5⋅x.}) ⅆx and apply U-Substitution to produce
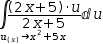 ∫(2⋅x+5)⋅u÷(2⋅x+5) ⅆ(u(x)→x^2+5⋅x).
∫(2⋅x+5)⋅u÷(2⋅x+5) ⅆ(u(x)→x^2+5⋅x).
The strategy then is to remove all terms in x. In this case, the
strategy is achieved by
Simplify 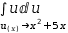 ∫u ⅆ(u(x)→x^2+5⋅x).
∫u ⅆ(u(x)→x^2+5⋅x).
The decoration on the integral is called the u-integrator. The name of the
function in the u-integrator is generated so as not to be the same as any
variable in either the integrand or the integrator.
The right side is the original subject of u-substitution. When a
decorated integral is integrated, the result also contains the decoration.
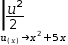 |u^2÷2 ⅆ(u(x)→x^2+5⋅x).
|u^2÷2 ⅆ(u(x)→x^2+5⋅x).
When a decorated integration is
simplified, the right side of the decoration is substituted into the integrand:
 (x^2+5⋅x)^2÷2.
(x^2+5⋅x)^2÷2.
You can prove the final result is correct by taking its
derivative and simplifying it.
Decorated integrals use a special form of syntax. Normally, the
integrator is coded as a single variable in the second operand to the
integral, the one following ⅆ. A decorated integral codes the
integrator using the form
(u(x)→expression). A simpler form is also accepted:
(u=expression). When the latter form is used, the arguments to the u-integrator are
inferred from variables in the expression.
Note the use of parenthesis in the second operand of a decorated
integral. If omitted, the expression
∫u ⅆu(x)=x^2+5*x
would be parsed as an equation.
Try to simplify the following integrals:
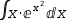 ∫x⋅ⅇ^x^2 ⅆx
∫x⋅ⅇ^x^2 ⅆx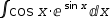 ∫cos x⋅ⅇ^sin x ⅆx
∫cos x⋅ⅇ^sin x ⅆx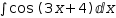 ∫cos (3⋅x+4) ⅆx
∫cos (3⋅x+4) ⅆx ∫1÷(1-2⋅x) ⅆx
∫1÷(1-2⋅x) ⅆx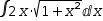 ∫2⋅x⋅√(1+x^2) ⅆx
∫2⋅x⋅√(1+x^2) ⅆx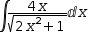 ∫4⋅x÷√(2⋅x^2+1) ⅆx
∫4⋅x÷√(2⋅x^2+1) ⅆx
4.4.2.1 Integrator Substitution
The integral 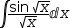 ∫sin (√x)÷√x ⅆx is solved using the third variation of u-substitution (§3.4.1),
called integrator substitution. From the integral, extract the subexpression
∫sin (√x)÷√x ⅆx is solved using the third variation of u-substitution (§3.4.1),
called integrator substitution. From the integral, extract the subexpression 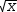 √x using selection and
√x using selection and  and
use it to add
and
use it to add 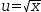 u=√x to the algebra display. Select and Isolate x to produce the auxiliary expression
u=√x to the algebra display. Select and Isolate x to produce the auxiliary expression 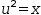 u^2=x.
Select the integrator
u^2=x.
Select the integrator 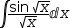 ∫sin (√x)÷√x ⅆx and apply U-Substitution to produce
∫sin (√x)÷√x ⅆx and apply U-Substitution to produce 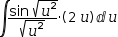 ∫sin (√(u^2))÷√(u^2)⋅(2⋅u) ⅆu.
This simplifies to
∫sin (√(u^2))÷√(u^2)⋅(2⋅u) ⅆu.
This simplifies to 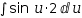 ∫sin u⋅2 ⅆu and integrates to
∫sin u⋅2 ⅆu and integrates to 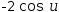 -2⋅cos u. Isolate u in the auxiliary expression and
substitute it into the integration to yield
-2⋅cos u. Isolate u in the auxiliary expression and
substitute it into the integration to yield 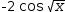 -2⋅cos (√x).
-2⋅cos (√x).
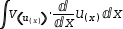
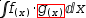
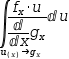
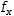
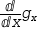
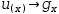
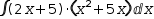
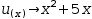
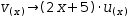

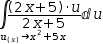
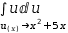
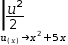

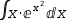
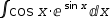
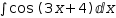

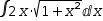
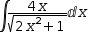
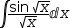
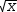
 and
use it to add
and
use it to add